Introduction
Overfitting and underfitting are two common problems that can occur when training a machine learning model. Understanding these concepts is crucial for building accurate and reliable models that generalize well to new, unseen data. In this article, we will define overfitting and underfitting, explain the causes of these problems, and discuss how to prevent and mitigate them.
But before diving into the concepts of overfitting and underfitting let’s understand some basic terminologies:
Signal - In machine learning, the term "signal" refers to the useful information or patterns in the data that the model is trying to learn.
Noise - The term "noise" refers to the irrelevant or random variations in the data that can interfere with the model's ability to learn the signal.
Bias - The term "bias" refers to the systematic error or deviation of the model's predictions from the true values. A model with high bias is said to be underfitting, meaning it is too simple and unable to capture the complexity and patterns in the data.
Variance - The term "variance" refers to the degree to which the model's predictions vary or fluctuate for different training data sets. A model with high variance is said to be overfitting, meaning it is too complex and is able to fit the training data too well, but performs poorly on new, unseen data.
To build accurate and reliable machine learning models, it is important to find a balance between bias and variance and to minimize the noise in the data.
Check out Bias and Variance in Machine Learning to gain better insights about bias and variance in machine learning.
What is overfitting?
Overfitting is a phenomenon that occurs when a machine learning model is too complex and is able to fit the training data too well, but performs poorly on new, unseen data. In other words, the model has learned the "noise" in the training data, rather than the underlying relationships and patterns. As a result, the model is not able to generalize to new data and makes poor predictions.
There are several factors that can contribute to overfitting, including
Too many features: If the model has too many input variables (features), it may be able to fit the training data too well, but not be able to generalize to new data. This is because the model has learned the noise in the training data, rather than the underlying relationships and patterns.
Lack of regularization: Some machine learning algorithms, such as neural networks and decision trees, have the ability to "memorize" the training data if they are not regularized. Regularization is a technique that adds a penalty to the model to prevent it from fitting the training data too well.
Insufficient training data: If the training dataset is small, the model may be able to fit the training data too well, but not be able to generalize to new data. This is because the model has not seen enough examples to learn the underlying relationships and patterns.
Here is a simple code which explains the concept of overfitting 👇
import matplotlib.pyplot as plt
import numpy as np
# Generate synthetic data for the regression model
X = np.linspace(0, 10, 100)
y = 2 * X + np.random.normal(0, 1, 100)
# Fit a linear regression model to the data
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(X.reshape(-1, 1), y)
# Generate predictions for the model
y_pred = reg.predict(X.reshape(-1, 1))
# Plot the data and the regression model
plt.scatter(X, y, label="data")
plt.plot(X, y_pred, label="regression")
# Overfit the model by adding polynomial features
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=5)
X_poly = poly.fit_transform(X.reshape(-1, 1))
# Fit a linear regression model to the overfitted data
reg_overfit = LinearRegression().fit(X_poly, y)
# Generate predictions for the overfitted model
y_pred_overfit = reg_overfit.predict(X_poly)
# Plot the overfitted model
plt.plot(X, y_pred_overfit, label="overfitted regression")
plt.legend()
plt.show()
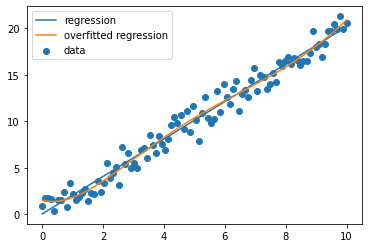
This code generates synthetic data for a linear regression model, fits a linear regression model to the data, and plots the data and the model. It then overfits the model by adding polynomial features and fitting a linear regression model to the overfitted data and plots the overfitted model as well. The resulting plot shows the data and both the regular and overfitted linear regression models, allowing you to visualize the overfitting of the model.
What is Underfitting?
Underfitting is the opposite of overfitting and occurs when a machine learning model is too simple and is unable to capture the complexity and patterns in the training data. As a result, the model performs poorly on both the training data and new, unseen data.
There are several factors that can contribute to underfitting, including
Too few features: If the model has too few input variables (features), it may not be able to capture the complexity and patterns in the training data.
Insufficient model complexity: Some machine learning algorithms, such as linear regression and logistic regression, have a limited capacity to capture complex patterns in data. If the training data is too complex, these algorithms may be unable to fit it accurately.
Insufficient training data: If the training dataset is small, the model may not have seen enough examples to learn the underlying relationships and patterns in the data.
Here's an example of how underfitting works 👇
import matplotlib.pyplot as plt
import numpy as np
# Generate synthetic data for the regression model
X = np.linspace(0, 10, 100)
y = np.sin(X) + np.random.normal(0, 0.5, 100)
# Fit a linear regression model to the data
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(X.reshape(-1, 1), y)
# Generate predictions for the model
y_pred = reg.predict(X.reshape(-1, 1))
# Plot the data and the regression model
plt.scatter(X, y, label="data")
plt.plot(X, y_pred, label="regression")
# Underfit the model by using a linear model to fit a non-linear function
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X.reshape(-1, 1))
# Fit a linear regression model to the underfitted data
reg_underfit = LinearRegression().fit(X_poly, y)
# Generate predictions for the underfitted model
y_pred_underfit = reg_underfit.predict(X_poly)
# Plot the underfitted model
plt.plot(X, y_pred_underfit, label="underfitted regression")
plt.legend()
plt.show()
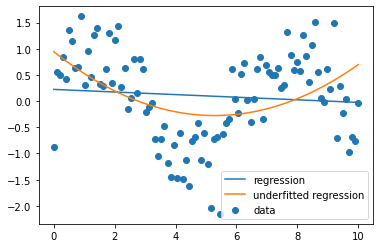
This code generates synthetic data for a non-linear function, fits a linear regression model to the data, and plots the data and the model. It then underfits the model by using a linear model to fit a non-linear function and plots the underfitted model as well. The resulting plot shows the data and both the regular and underfitted linear regression models, allowing you to visualize the underfitting of the model.
How to prevent and mitigate overfitting and underfitting
There are several techniques that can be used to prevent or mitigate overfitting and underfitting, including
Splitting the data into training and validation sets: One way to avoid overfitting is to split the data into a training set and a validation set. The model is trained on the training set, and its performance is evaluated on the validation set. This allows us to determine whether the model is overfitting or underfitting the data.
Using cross-validation: Another way to prevent overfitting is to use cross-validation, which involves training the model on different subsets of the data and evaluating its performance on the remaining data. This helps to ensure that the model is not overly dependent on any particular subset of the data.
Regularization: As mentioned earlier, regularization is a technique that adds a penalty to the model to prevent it from fitting the training data too well. This can help to prevent overfitting and improve the generalization of the model to new, unseen data. There are several types of regularization techniques, including L1 regularization, L2 regularization, and elastic net regularization. These techniques add a penalty term to the model's objective function, which encourages the model to simplify and reduce the complexity of the learned relationships. Regularization can be adjusted using a hyperparameter, which controls the strength of the penalty. By tuning the hyperparameter, it is possible to find the optimal balance between bias and variance and to prevent overfitting while still capturing the useful signal in the data.
Ensemble techniques: Ensemble techniques are machine learning methods that combine the predictions of multiple models to produce a more accurate and robust prediction. These techniques can be used to prevent overfitting and underfitting, as they can help to reduce the variance and bias of the model. There are several types of ensemble techniques, including:
Bagging: Bagging (short for bootstrapped aggregating) involves training multiple models on different subsets of the data, and then averaging or voting on their predictions. This can help to reduce the variance of the model, as the individual models are less likely to overfit the data.
Boosting: Boosting involves training multiple models sequentially, where each model is trained to correct the mistakes of the previous model. This can help to reduce the bias of the model, as the individual models are able to learn from the errors of the previous models.
Stacking: Stacking involves training multiple models, and then using a "meta-model" to combine their predictions. This can help to reduce both the bias and variance of the model, as the individual models and the meta-model are able to learn from the errors of the other models.
By using ensemble techniques, it is possible to build more accurate and robust machine learning models that are less prone to overfitting and underfitting.
Inference
In conclusion, overfitting and underfitting are common problems that can occur when training a machine learning model. Overfitting occurs when a model is too complex and is able to fit the training data too well, but performs poorly on new, unseen data. Underfitting is the opposite of overfitting and occurs when a model is too simple and is unable to capture the complexity and patterns in the training data. To prevent and mitigate overfitting and underfitting, it is essential to split the data into training and validation sets, use cross-validation, and apply regularization as needed. By understanding and addressing these issues, it is possible to build accurate and reliable machine-learning models that generalize well to new data.
Thanks for reading ♥️
